IGRT平台下图像登记技术应用初探
邹炼1,侯氢1△,柏森2
(四川大学 1. 原子核科学技术研究所 辐射物理及技术教育部重点实验室 成都 610064;
2. 华西医院放疗科 成都 610041)
在IGRT平台下,医用加速器集成了KV级的锥形束CT,它能够获取病人在治疗时的解剖信息。在当前临床应用中,首先把定位CT获得的三维病人数据与在线采集的锥形束CT数据进行图像登记,得出病人真实摆位与做计划用的摆位之间的相对位移信息。然后调整治疗床的位置,实现更精确的治疗。图像登记的过程在IGRT平台下是一个非常关键的一环,它的结果好坏直接影响我们的治疗精度。图像登记的质量保证是我们IGRT平台下非常重要的一个环节。所以研究临床上所使用的图像登记算法的性质是很有必要的。
我们所用的图像登记方法与医科达公司的Synergy™ system 中所用的图像登记方法属同一类型即基于图像灰度值得方法。为了对照的目的,图像登记算法采用了两种,一种是基于最小平均方差目标函数的登记方法[1],一种是规一化的最大相关系数目标函数的登记方法[2][3]。这两种登记方法的优化算法都采用正规步长梯度下降方法。测试图像包括:基准图像是标准的测试图像;平移后的图像就是把基准图像简单的沿X轴平移13mm,Y轴平移17mm
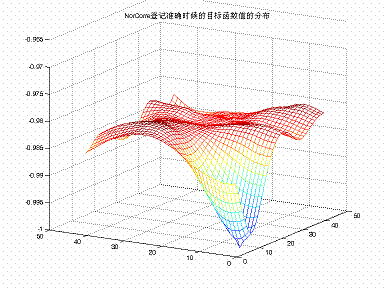
;旋转后的图像就是原基准图像绕图像的中心旋转5度得到的。通过选定不同的感兴趣区域的位置和改变感兴趣区域的大小来考察图像登记方法的表现。在只考虑平移的登记任务中,我们在设定的参数空间穷举计算目标函数值,最后再找出最小值的位置,这个位置就是我们的登记结果。这种算法在这我们姑且称之为穷举算法。这样我们就可以方便的比较登记正确时候的目标函数值的空间分布和登记错误时的目标函数值的空间分布[4]。
我们研究发现感兴趣区域的位置以及感兴趣区域的大小对图像登记方法结果的影响非常显著,而且对于不同的受登记图像(不同部位的图像),感兴趣区域的位置选取,大小选取对结果的影响还很不一样。对于穷举算法,感兴趣区域的位置以及区域大小的选取虽然没有影响但是我们在实际应用中,不可能用穷举算法。从穷举算法得到的目标函数空间分布来看,感兴趣区域的位置选取,大小选取主要影响目标函数值的分布。感兴趣区域位置选的不好或区域大小不合适,就会在目标函数值的分布中产生很多局部最小点,有些还很深。这样就会导致登记算法收敛到局部最小点。我们认为:针对这样一个较理想化的测试实例,都发现感兴趣区域的选取对结果的影响非常大,那么对于临床上那些复杂得多的登记任务,这种影响必定更加显著。我们有必要对临床上各种典型的治疗区域的图像登记任务中所选用的感兴趣区域的位置以及区域的大小的选取作一个仔细的对比研究[5][6]。
关键词:调强放疗,图像引导放射治疗,图像登记,锥形束CT,摆位误差
参考文献:
[1]
S. Umeyama, “Least-squares estimation of transformation parameters between two
point patterns,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 13, pp. 376–380,
1991.
[2]
P. A. van den Elsen, E.-J. D. etc. , “Grey value correlation techniques used
for automatic matching of CT and MR brain and spine images,” Visualization in
Biomedical Computing 1994, vol. Proc. SPIE 2359, pp. 227–237, 1994.
[3]
[4]
G. P. Penney, J. Weese, et al. “A comparison of similarity measures for use in
2D-3D medical image registration”. IEEE Transactions on Medical Imaging,
17(4):586–595, 1998.
[5] Pallotta
S, Bucciolinia M, et al. “Accuracy evaluation
of image registration and segmentation tools used in conformal treatment
planning of prostate cancer” Computerized
Medical Imaging and Graphics 30 (3): 213-213 APR 2006
[6]
Uhlemann F, Morgenstern U, Steinmeier R. “Objective evaluation
of three dimensional image registration algorithms Tools for optimization and
evaluation” Methods of Information in Medicine 43 (4): 367-370 2004