计算机电子射野影像模拟在放疗质控中作用的研究

Research on application of CMEPI in radiotherapy QC

浙江省肿瘤医院物理室 王彬冰 狄小云

近年来电子射野影像系统(electronic portal imaging device, EPID)用于代替传统的胶片射野影像，作为日常放射治疗中摆位校验和剂量误差分析。EPID的图像模拟和基于EPID的治疗实施验证也被广泛报道[1-4]。主要包括：通过比较实际测量的EPID图像和模拟计算的EPID图像的差别，可以验证实际照射时病人的摆位正确与否；EPID图像可以用于验证调强放射治疗中多叶准直器的叶片位置；同时可以为三维剂量重建提供输入数据，以判断照射时的剂量施与是否正确。因此，电子射野影像对临床治疗精度的控制有重大意义。而用计算机模拟得到的电子射野影像(Computer Modeling of Electronic Portal  Imaging CMEPI )比DDR影像更接近于真实的射野影像，可以替代DRR作为放射治疗中验证摆位误差的方法。作者在这方面做了一些研究，报道如下：

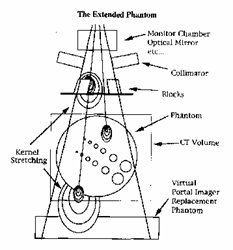
目的：使用微分卷积积分剂量模型模拟计算实际照射时射野影像系统平面上的二维剂量分布，预测实际治疗时的电子射野影像系统的图像，使该模拟影像可以被用于日常摆位误差的验证。方法和材料：使用微分卷积积分剂量模型[5]，计算射线穿过模体后最终照射到模体底部成像平面上的剂量分布。实验在模拟扩展水箱和真实人体CT数据中进行，照射条件为SSD=100cm，FSZ=10cm×10cm均匀束，6MV-X线（多能谱）。①在均匀水模中拟合能谱后，用微分卷积积分剂量模型计算的百分剂量分布(PDD)和我们实际测量的数据相比较，如图1所示。②然后用扩展水箱的方法[6]，即把模体以下到成像平面之间的空气作为剂量计算模体的一部分，对真实人体在CT模拟机下进行扫描，影像在计算机上进行三维重建，用剂量模型计算模体经重建后在成像平面处的二维剂量分布，并把该二维剂量分布用灰度图表示出来。

 

 

 

 

 

 

 


图1　扩展水箱模型示意图

 

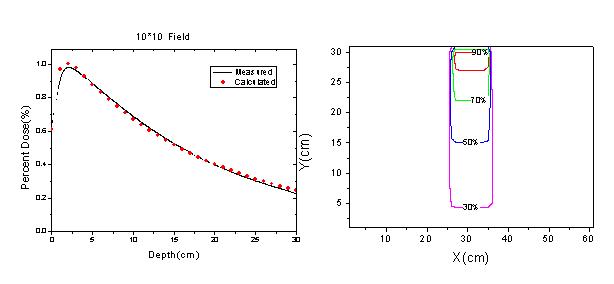
结果：图2显示用微分卷积积分剂量模型拟合6MV-X线能谱后得到的PDD和实际测量的PDD符合性较好，证实所使用的剂量模型有较高的计算精度。图3显示模拟计算的射野影像和实际的EPID射野影像很相似。

 

 

 

 

 

 

 

 


           a)                                                 b)

图2a 模拟计算的PDD和实际测量的PDD    图2b 10cm×10cm射野沿z方向中心平面剂量分布

 

 

 

 

 


图3 射野平面剂量灰度图

结论：由Mackie TR等人提出的微分卷积积分剂量模型是一种真正的三维光子剂量计算方法，该方法有较好的计算精度。其基本原理是空间任何点的剂量可以表示为原射线剂量分布与一个积分核的卷积积分。

这里表示原束光子在处单位质量释放的能量（TERMA），卷积核由蒙特卡罗方法模拟得到。使用微分卷积积分剂量模型计算成像平面的二维剂量分布，把该剂量分布用灰度图表示就得到模拟的射野影像。

    计算机模拟的射野影像是在治疗计划设计标准体位下得到的，通过比较模拟射野影像和实际得到的有摆位误差的射野影像，可以作为日常放疗中验证摆位误差的有效手段用于治疗时的质量控制，特别在没有EPID的单位可以将模拟射野影像结合验证片影像来验证摆位误差。同样也可以计算成像平面上得到的射野影像, 预测出存在一定摆位误差时的剂量差异。把模拟射野影像平面的剂量和实际得到的射野影像图的像素灰度定标后，可以用EPID记录出射的二维剂量分布，通过反投影迭代算法，重建照射时人体内三维剂量分布。比较计划阶段预期的人体内三维剂量分布和照射时实际得到的三维剂量分布，对整个照射阶段的剂量施与有更准确的控制。模拟射野影像用于放疗中的质量控制还有待近一步研究，我们将在以后的工作中进行。

参考文献

[1] M Wending，Robert J.W.Louwe,et al. “Accurate two-dimensional IMRT verification using a back-projection EPID dosimetry method”,  Med. Phys. 33 (2):259-273,(2006)

[2]R. J. W. Louwe, E. M. F. Damen, et al.  “Three-dimensional dose reconstruction of breast cancer treatment using portal imaging”, Med. Phys. 30 (9): 2376-2389, Sep 2003

[3] B.Warkentin, S.Steciw, S.Rathee, et al. “Dosimetric IMRT verification with a flat-panel EPID”, Med. Phys. 30(12): 3143-3155, Dec 2003

[4] W.J.C.van Elmpt, S.M.J.J.G.Nijsten,a_ B.J.Mijnheer,et al. “ Experimental verification of a portal dose prediction model”, Med. Phys. 32(9): 2805-2818 Sep 2005

[5] T.R.Mackie,J.W.Scrimger,et al. “A Convolution method of calculating dose for 15-MV X rays”, Med.Phys.12 (2),Mar/Apr 1985

[6] T.R.McNutt, T.R.Mackie, P.Reckwerdt, et al. ＂Calculation of portal dose using the convolution/superposition method＂，Med. Phys. 23 (4): 527-535 APR 1996